面向时间序列事件的动态矩阵聚类方法

马瑞强，宋宝燕，丁琳琳，王俊陆

辽宁大学 信息学院，沈阳110036

近年来，随着信息化技术的快速发展，金融、生物、气象、医学等各个领域产生了大量的时间序列数据[1]，挖掘数据中的潜在价值对决策者具有重大的指导作用。聚类[2-4]作为一种无监督学习[5-6]方法，由于其事先无需对任一样本打类别标记，在分析数据的内在关系及蕴含的信息、知识等方面发挥着至关重要的作用。时间序列数据本身具有伪事件、持续性及漂移性等复杂结构特征，现有方法多直接对数据集中结构复杂的持续事件聚类，未将聚类对象进行转化，聚类结果准确性低且效率差，因此如何设计一种精准高效的时间序列事件聚类[7]方法，一直是流式数据挖掘[8-9]领域研究的难点。

针对这些问题，本文提出一种面向时间序列事件的动态矩阵聚类方法RDMC（RDS dynamic matrixbased clustering），通过精准、高效地构建RDS（representative and diversifying sequences）与数据集的距离矩阵，将对原始数据集的聚类转化为对动态化矩阵的聚类，实现时间序列事件的有效划分。本文的主要贡献如下：

（1）基于事件r近邻密度和反向近邻数构建事件近邻评价体系，依据评价值优劣衡量事件的代表性；

（2）在此基础上，提出事件近邻评分的后向差分计算策略，依据差分结果确定评分边界，通过近邻评分与边界值的大小关系构建RDS 候选集，提高RDS选取效率；

（3）综合RDS的双重约束条件，提出基于组合优化法最优解集筛选策略，实现RDS的高效查找；

（4）针对时序事件聚类准确率低的问题，提出基于K-means 的矩阵聚类方法，对RDS 与数据集的动态化距离矩阵聚类，最终得到事件的类别标签。

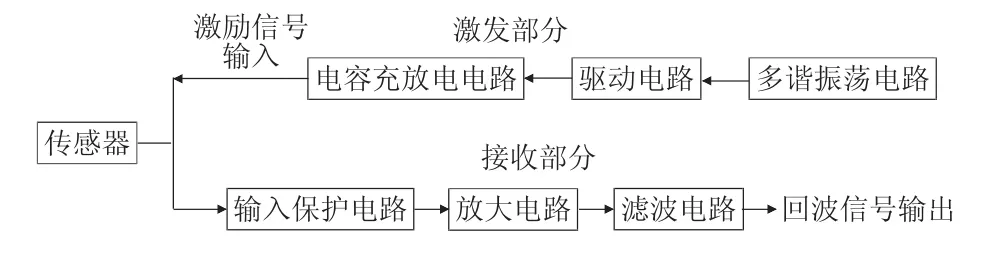
图1为RDMC方法结构示意图。

Fig.1 Schematic diagram of RDMC structure图1 RDMC方法结构示意图

1 相关工作

目前，许多专家学者对时间序列事件聚类方法进行了深入研究，取得了一定的研究成果。

Euán等人[10]提出基于谱密度[11]以及全变分距离[12]的聚类方法，通过事件的相似振荡行为构建类簇，该方法没有对原始数据集进行转化，直接对时间序列事件聚类，受事件的复杂结构影响，聚类准确率低；Azencott 等人[13]提出在大规模时间序列数据上的自动聚类方法，通过随机梯度下降法[14-15]最小化衡量聚类质量的代价函数，从而自动生成最优化类簇，由于代价函数的优化过程耗时过长，该方法的聚类效率较差；郑建炜等人[16]提出联合拉普拉斯正则项[17]和自适应特征学习方法，能够同时进行特征选择和数据聚类，但该方法需人工设定多个参数，参数的不同取值直接影响聚类结果的准确率；张东月等人[18]提出基于网格耦合和核心网格的聚类方法GCStream，通过网格耦合更精确地表达数据之间的相关性，但该方法建立的网格要求边长相等，无法适用于结构复杂的时间序列数据；Zakaria 等人[19]提出利用数据集中具有特征性的局部形状（U-Shapelets）进行聚类的方法，方法具有较高的准确性，但由于提取U-Shapelets的时间复杂度过高，导致聚类效率极低；Madiraju 等人[20]提出深度时间聚类方法（deep temporal clustering，DTC），该方法利用一个自动编码器降低时间维数并通过一个新颖的时间聚类层进行聚类分配。迭代训练时间聚类层时，优化目标为最小化预测分布和目标分布的KL 散度损失[21-22]，目标分布通过预测分布进行计算并在每次迭代时更新，这导致该方法存在不稳定性，聚类准确性波动较大。

综上，本文对时间序列事件聚类进行了深入研究，针对现有聚类方法的不足，综合考虑事件的复杂结构特征，提出一种基于RDS 的时间序列事件聚类方法，在确保聚类准确性的同时提高聚类效率。

2 RDS候选集选取

时间序列事件是在时间域上满足一定条件的一系列离散数据点组成的序列。相同类型的事件通常都具有相同或相似的特征规律。提出事件近邻评价体系构建方法，依据评价值的优劣衡量事件的代表性，提出后向差分法确定近邻评分边界值，通过边界值与评价值的大小关系构建RDS候选集。

2.1 事件近邻评价体系构建

提出RDS 及其候选集概念，并基于事件近邻密度和反向近邻数构建事件近邻评价体系，通过评价值准确衡量数据集中任意事件的代表性。RDS如定义1所示。

定义1（RDS）给定时间序列事件数据集T={t1,t2,…,tn}，ti(1 ≤i≤n)为多个离散点集合构成的一个持续事件，RDS 为从T中选出的可最大化地代表不同类簇且差异性最大的k(1 ≤k≤T)个事件，其中的一个事件记为RDSi(1 ≤i≤k)。

最大化地代表不同类簇是指RDSi分别与不同类簇的相似性最大，差异性最大是指多个RDSi之间的相似性最小。图2 为RDS 定义示意图，数据集T被划分为四个类簇C1～C4，每个类簇包含的事件如蓝色小圆圈所示，T中最佳的RDS 如红色小圆圈所示。其中，RDS1与类簇C1中任一事件的距离d1较小，使得它与C1的整体相似度最大，即它可最大化地代表C1；同理，RDS2、RDS3可分别最大化地代表C2、C3。RDS1～RDS3间的距离d4～d6均较大，即它们在最大化地代表T中不同类别事件的同时，满足互相之间的差异性最大。

Fig.2 Schematic diagram of RDS definition图2 RDS定义示意图

RDS 选取策略影响事件聚类效率，直接从数据集T中选取的代价过高，因而先构建其候选集，再从候选集中查找k个代表性与差异性同时最大的事件构成RDS。

RDS候选集C表示从数据集T中选择的具有代表性的m个事件的集合，即C={t1,t2,…,tm}，ti(1 ≤i≤m)表示一个事件，且k≪m≪n，k表示RDS 里包含的事件数量，n为T的大小。所选择的一个事件必须与某一类簇的相似度较高，但多个事件之间不要求差异性较大。

事件大多具有漂移性等复杂的结构特征，为准确衡量它们之间的相似度，给出DTW（dynamic time warping）距离度量方法。

若有两个时间序列事件t1和t2，长度分别为t1和t2，记规整路径W={w1,w2,…,wr}，其中max(t1,t2)≤r≤t1+t2，wr的形式为(i,j)，i为t1中的一个元素，j为t2中的一个元素。令t1和t2的代价矩阵为D，则D中的一条路径为：

其中，ED(i,j)为i和j的欧式距离，最后得到t1和t2的DTW距离为：

以下，先构建事件近邻评价体系，通过评价值衡量数据集T中事件的代表性。事件r邻域的定义如下。

定义2（r邻域）给定数据集T，事件t的r邻域NNr(t)定义为与t距离最近的r个事件的集合，即：

其中，d(t,x)表示t与事件x的DTW距离，dr(t)表示t与其他事件间的第r近邻DTW距离。对于一个事件t，用t的近邻密度量化t与其r邻域内的事件的总体相近程度。

定义3（近邻密度）给定事件t的r邻域NNr(t)，t的近邻密度P(t)定义为：

P(t)越大，表示t与所有在其r邻域内的事件的整体相似性越高；反之，则相似性越低。此外，通过反向近邻数可从反向角度衡量事件t与其他事件的相近程度。

定义4（反向近邻数）反向近邻数Nb(t)表示在对T中的每个事件计算其r近邻距离的过程中，事件t被其他事件近邻的总次数。即：∀x∈T，若∃t∈NNr(x)，则Nb(t)=Nb(t)+1，1 ≤r＜n。

Nb(t)越大，表明t被更多的事件近邻，反向说明t与更多事件的距离越近，即相似性越高。在近邻密度和反向近邻数的基础上，提出事件近邻评分的概念，同时从正反两方面综合衡量事件t与其他事件的整体相似性。

定义5（近邻评分）给定事件t的反向近邻数Nb(t)与近邻密度P(t)，t的近邻评分S(t)为ln(Nb(t)+1)与P(t)的乘积，即：

公式中，通过对Nb(t)取对数缩小其尺度，使其变化更平稳，由于Nb(t)可能为0，对其加1，可避免对数计算值出现负数，即使得ln(Nb(t)+1)≥0。公式表明，给定t的r邻域NNr(t)，若t的反向近邻数Nb(t)与近邻密度P(t)越大，则S(t)越大，表明t与更多事件相似，即t是具有代表性的事件。

2.2 基于后向差分法的RDS候选集构建

在近邻评价体系的基础上，提出近邻评分的后向差分计算策略，依据差分计算结果快速筛选RDS候选集。

不同事件的反向近邻数与近邻密度均相差较大，使得近邻评分的计算值不在同一尺度下，需将其归一化至[0,1]区间。以来自UCR 数据库的Plane 数据集为例，对该数据集中的所有事件计算近邻评分，归一化并排序，得到图3（a）中的近邻评分示意图。

如图3中所示，候选集C中事件的近邻评分高于正常事件，故C中的事件均位于高评分区域，正常事件处于低评分区域，且在二者的边界处，近邻评分的跳跃幅度大。基于此，本文提出近邻评分的后向差分计算策略，通过比较差分值的大小确定边界并构建候选集，后向差分计算公式如下：

∇S(t)=S(t)-S(t-1) （6）

其中，∇S(t)为差分算子，S(t)与S(t-1)为两个相邻事件。图3（b）为近邻评分的后向差分计算结果，从中可看出，差分最大值所在点正好位于图3（a）中评分出现较大跳跃的位置。

RDS候选集C构建的具体过程如算法1所示。

算法1构建C算法

输入：数据集T，阈值参数φ。

输出：RDS候选集结果C。

1.初始化：r=0，N(r)=0；

2.对T中的每个事件计算第r近邻w；

3.Nb(w)←Nb(w)+1，NNr(t)←NNr(t)⋃{w}；

4.依据式（5）计算t的近邻评分S(t)；

5.若Nb(t)==0，则N(r)=N(r)+1；

Fig.3 Schematic diagram of r-nearest neighbor score and its difference图3 近邻评分及其差分示意图

6.若(N(r-1)-N(r))/N(r-1)＜φ，转至步骤7，否则,令r=r+1，转至步骤2；

7.对S(t)进行归一化处理并排序；

8.依据式（6）计算S(t)的后向差分D，记最大值的索引值为max；

9.若S(t)>S(max)，则t∈C，令C=C⋃t，否则,t∉C；

10.返回候选集结果C。

首先，在构建T中所有事件r邻域的过程中，对每个事件t计算其第r近邻序列w，将w的反向近邻数Nb(w)加1，并将w添加至t的r邻域NNr(t)，计算t的近邻评分S(t)。此时，统计T中事件的反向近邻数等于0的数量N(r)，若N(r)的下降率小于给定的阈值φ（0 ≤φ≪1，一般取[0,0.1]之间的数)，则r邻域构建完成，迭代结束，否则继续构建第r+1 邻域；如图4所示，刚开始时，随着r增大，N(r)快速减小；当r增至一定大时，N(r)减小的速度趋于平缓并最终减小至0。N(r)平缓减小时，r获得最佳截止值。以某一事件t为例，若r再增大，将导致与t相距较远的事件被错误添加至t的r邻域，近邻关系建立不当将使得近邻评分值无法正确衡量t的代表性。其次，对归一化并排序处理后的近邻评分S进行差分计算，计算结果D中的最大值索引记为max。最后，位于max侧的事件属于RDS候选集，将它们添加到C，返回C。

Fig.4 Schematic diagram of change trend of N图4 N的变化趋势示意图

3 时间序列事件聚类

在候选集C的基础上，提出基于组合优化的RDS最优选取方法，动态构建RDS与数据集的距离矩阵，提出基于K-means的矩阵聚类方法，实现事件的类别划分。

3.1 最优RDS解选取

由定义1 可知，RDS 需同时满足“相似性”与“差异性”两个条件，故RDS的选取为多条件约束最优解问题，可通过组合优化的方法求解，依据近邻评分计算候选集中所有可行解的质量指标QI，通过比较QI的大小得到最优解。

记C中任意k个事件的一个组合为RDS 的一个可行解，所有可行解构成集合F，对于特定的一个可行解f∈F，f中k个事件的近邻评分均值记为u，它们之间的距离均值记为v。即：

u、v现不在同一尺度下，将其规格化至[0,1]区间，使二者具有可比性。此外，为准确量化可行解f的选取质量，本文提出质量指标的概念。

定义6质量指标QI（quality index）用于同时衡量RDS 的一个可行解f的双重约束条件，计算公式如下：

其中，0 ＜α＜1，系数α用于均衡u与v的占比，默认情况下，α=0.5。u,v越大，则QI(f)越大，表明f的“相似性”与“差异性”越大，选取质量越高。当QI(f)最大时，RDS取得最优解o，即：

综上所述，最优RDS解选取过程如算法2所示。

算法2选取RDS算法

输入：数据集T，阈值参数α，RDS大小k。

输出：RDS最优解o。

1.由算法1获得候选集C；

2.将从C中取k个事件的所有可行解记为F；

3.对于每一个可行解f，根据式（5）、式（6）计算u,v，并将其归一化；

4.根据式（9）计算f的QI；

5.根据式（10）求得最优解的o。

图5 为Plane 数据集的类簇示意图，该数据集包含210条数据，分为7个类别。

Fig.5 Schematic diagram of clusters of Plane data set图5 Plane数据集的类簇示意图

对该数据集上构建候选集C后，当k取2时，得到如图6所示的RDS选取结果示意图。

3.2 基于K-means的矩阵聚类

在3.1 节选出的RDS 的基础上，通过动态构建RDS 与数据集的距离矩阵进行聚类对象的转化，提出基于K-means的矩阵聚类方法，根据矩阵聚类结果得到事件的类别标签。

RDS与数据集的距离矩阵M的形式如下所示。

Fig.6 Schematic diagram of RDS selection result图6 RDS选取结果示意图

M的大小为[n,i]，i≤k，表示RDS 中实际参与聚类的事件数量，n表示数据集T中所有事件的数量，M中的元素mji表示RDSi与T中事件j的距离。

矩阵M的一个重要属性是其蕴含事件间的相对距离大小。图7为在Plane数据集上选出的RDS与数据集的距离矩阵示意图，图中的每一个点的坐标值表示一个事件与RDS1以及RDS2的距离，如点(X,Y)表示一个事件与RDS1的距离为0.337，与RDS2的距离为0.039。由于各个事件间的相对距离大小的不同，该距离矩阵间接地把原始数据集划分成了7个类别，对矩阵M聚类将实现对原始数据集的类别划分。

Fig.7 Schematic diagram of distance matrix between RDS and data set图7 RDS与数据集的距离矩阵示意图

此外，M不是由RDS与数据集的距离向量直接构成，而是逐步扩展、动态构建生成，其目的是进一步提高聚类的准确率和效率。当计算RDSi与数据集的距离向量后，将该向量添加为矩阵M的一列横向扩展M，根据当前的聚类纯度Pur的大小，再决定是否需要继续拓展M以及进行聚类操作。聚类纯度的计算公式如下：

其中，n表示总的事件个数；C={c1,c2,…,cj}表示真实的类簇划分；Ω={w1,w2,…,wk}表示当前聚类的类簇划分。

基于K-means 的矩阵聚类方法的具体过程如算法3所示。

算法3 聚类算法

输入：数据集T，阈值参数τ，RDS大小k1，事件类别数k2。

输出：事件类别标签Labels。

1.初始化：i=0，iters=1，MaxIters=50；

2.由算法2获得候选集RDS最优解R；

3.Whilei＜k1:

4.计算第RDSi与T的距离向量dist;

5.Dist=[Dist dist]；

6.[Labels,Centroids]=K-means(Dist,k2)；iters++;

7.若iters<MaxIters，转至步骤6；

8.CP(i)=1-Pur(Labels(i-1),Labels(i))；

9.若CP(i)＜τ，转至步骤11；

10.i++；

11.返回聚类结果Labels(i)。

首先，构建候选集C并得到RDS 最优解R；其次，迭代地进行聚类过程（4～10 行），当i＜k1时，计算RDSi与T的距离向量dist并将其横向添加到Dist里，Dist此时为RDS 中前i个事件与T的距离矩阵。使用K-means 对Dist聚类，为使聚类结果更准确，Kmeans 运行了多次。记聚类纯度Pur的变化量为CP（Change inPur），假定第i-1 次循环时得到的聚类标签是正确的，则由公式可得，第i次循环时对应的CP(i)=1-Pur(Labels(i-1),Labels(i))。当CP小于τ（0 ≤τ≪1，一般取[0,0.1]之间的数）时，循环结束。随着参与构建矩阵Dist的RDS的数量的增加，Dist里包含更详尽的事件间的相对距离信息，促使RI呈现上升趋势，当CP较小时，表明此时已得到最佳聚类结果，无需再继续进行聚类过程；最后，返回通过聚类得到的事件类别标签。

4 实验分析

实验平台为Intel®i5-6500 3.20 GHz处理器，8 GB内存，Windows 10（64 bit）操作系统。从UCR公开数据库中选取6个数据集进行实验，如表1所示。从聚类准确率、聚类可靠性、时间效率等方面验证本文提出的RDMC 方法的有效性，对比方法为K-means、DBSCAN（density-based spatial clustering of applications with noise）、Spectral、U-Shapelets 等。阈值参数τ取0.05，φ在两个较大数据集FordA 与StarLightCurves上取0.07，在其他小规模数据集上取0.03。

Table 1 Experimental data set表1 实验数据集

4.1 聚类准确率对比

本节在表1 的基准数据集上评估RDMC 方法的聚类准确率，使用RI（Rand index）作为评价指标，RI计算公式如下：

其中，TP表示属于同一类且被分到同一簇中的事件数量；TN表示属于不同类且被分到不同簇中的事件数量；FP表示属于不同类但被分到同一簇中的事件数量；FN表示属于同一类但被分到不同簇中的事件数量。0 ≤RI≤1，RI值越大，聚类准确率越高。表2为RDMC方法与各对比方法的RI结果对比。

Table 2 Comparison of clustering accuracy(RI)表2 聚类准确率（RI）对比

由结果可知，RDMC 方法在4 个数据集上的RI高于其他方法，在所有数据集上都有RI≥0.84。此外，相对于K-means、DBSCAN、Spectral、U-Shapelets方法，RDMC 方法在所有数据集上的准确率平均提升了12%、22%、23%、36%。因此，RDMC 方法具有更高的准确率。

4.2 聚类可靠性对比

本节在Plane数据集上通过实际的聚类结果对比RDMC 方法与其他四种方法的聚类可靠性，聚类所得类别标签对比如图8所示，其中，Real组的七幅子图表示所有事件的真实所属类别，其余五组中的七幅子图分别表示各聚类方法将数据集实际所划分的类别。

从图8 中可看出，K-means 方法对类4、6、7 的划分基本正确，但类1、2中的部分事件应属于类5，理应属于类1、2 中的部分事件被错误地分到了类3；DBSCAN对各个类的划分大致正确，但该方法基于密度聚类，聚类质量高度依赖于参数邻域半径Eps和Eps内的最少事件数Minpts的取值，不在各个类簇任一事件邻域半径内的事件均被识别为噪声，这导致有相当一部分正常事件被误划分为噪声数据；Spectral、U-Shapelets 与K-means 类似，聚类结果中均有部分事件被错误归类；RDMC 方法的预测标签接近于真实类别标签，仅有极少数事件未被正确聚类。综上，RDMC方法比其他方法具有更优的聚类质量，可靠性更高。

4.3 聚类效率对比

本节验证RDMC 方法的聚类效率，各个方法在不同数据集上的具体运行时间对比如图9 所示，UShapelets 方法的运行时间比其他方法高出几个数量级，故在图中使用同一横坐标、不同的纵坐标对比几种方法的时间消耗。

由实验结果可发现，K-means 耗时最少；Spectral构建相似性矩阵并进行特征值分解的代价较高，导致其聚类效率较低；DBSCAN 的时间主要花费在查找Eps 邻域内符合条件的事件，其代价明显低于Spectral；RDMC 的耗时高于K-means，低于DBSCAN与Spectral；U-Shapelets提取过程极为漫长，使得该方法的运行时间远远高于其他方法。

特别地，在较大数据集FordA、StarLightCurves上，虽然K-means的效率高于RDMC，但由4.1节的实验结果可知，RDMC 在这两个数据集上的聚类准确率高于K-means，一个可能的原因是这两个数据集中的部分序列存在漂移性，其结构较复杂，RDMC把对原始数据集的聚类转化为对矩阵的聚类后，极大地减少了结构失真问题对准确率的影响。

Fig.8 Comparison of class labels图8 聚类所得类别标签对比

Fig.9 Comparison of running time图9 运行时间对比

总之，RDMC 具有良好的聚类效率且比其他方法更适合处理具有复杂结构的持续事件。

4.4 参数敏感度分析

本节对RDMC方法的阈值参数φ与τ的敏感性进行分析并讨论其合理取值，φ与τ在不同取值情况下的聚类准确率如图10、图11所示，聚类准确率使用式（11）中的Pur来衡量。φ与τ均近似等于0，二者的取值均限制在[0,0.1]之间。

Fig.10 Effect of value of φ on clustering purity图10 φ 的取值对聚类纯度的影响

Fig.11 Effect of value of τ on clustering purity图11 τ 的取值对聚类纯度的影响

由结果可知，随着φ增大，小数据上的Pur先保持稳定后小幅度减小，大规模数据集上的Pur基本不变。φ对Pur的影响与数据集大小有关，若数据集规模较大（事件数量较多），则在算法1 中，相距较远的事件不会被轻易错误添加至r邻域，反之，则容易错误添加至r邻域。因此，在小规模数据集上，φ取[0,0.05]之间的数，确保聚类准确性；在大数据集上，φ的取值最好在[0.05,0.08]之间，保证聚类准确性的同时，提高聚类效率（φ越大，r邻域构建过程的迭代次数越少）。

而随着τ增大，Pur在所有数据集上均先保持稳定后缓慢减小。这是因为τ决定聚类过程（算法3）何时结束，其越小，Pur越高，但效率会小幅降低。因此，τ的最佳取值在[0.04,0.06]之间。

5 结论

本文对时间序列事件聚类进行了深入的研究，针对现有聚类方法聚类准确度低、效率差等问题，提出一种面向时间序列事件的动态矩阵聚类方法。首先，提出事件近邻评价体系，实现事件代表性的有效衡量；根据近邻评分的后向差分计算策略界定评分高低，实现RDS候选集的快速构建，进而提高RDS选取的效率；其次，提出基于组合优化的选取方法，实现RDS的高效且最优查找；最后，针对直接对时序事件聚类的准确率低的问题，在动态地构建RDS 与数据集的距离矩阵的基础上，提出基于K-means的矩阵聚类方法，实现事件所属类别的正确划分。实验验证了所提方法的有效性。